Day 3 - Girls in Data Science

Day 3 - Girls in Data Science#

# Load libraries
library(ggplot2)
library(tidyverse)
library(tidymodels)
library(palmerpenguins)

── Attaching core tidyverse packages ─────────────────────────────────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ lubridate 1.9.3     ✔ tibble    3.2.1
✔ purrr     1.0.2     ✔ tidyr     1.3.1

── Conflicts ───────────────────────────────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

── Attaching packages ───────────────────────────────────────────────────────────────── tidymodels 1.2.0 ──

✔ broom        1.0.6     ✔ rsample      1.2.1
✔ dials        1.3.0     ✔ tune         1.2.1
✔ infer        1.0.7     ✔ workflows    1.1.4
✔ modeldata    1.4.0     ✔ workflowsets 1.1.0
✔ parsnip      1.2.1     ✔ yardstick    1.3.1
✔ recipes      1.1.0     

── Conflicts ──────────────────────────────────────────────────────────────────── tidymodels_conflicts() ──
✖ scales::discard() masks purrr::discard()
✖ dplyr::filter()   masks stats::filter()
✖ recipes::fixed()  masks stringr::fixed()
✖ dplyr::lag()      masks stats::lag()
✖ yardstick::spec() masks readr::spec()
✖ recipes::step()   masks stats::step()
• Use suppressPackageStartupMessages() to eliminate package startup messages

Attaching package: ‘palmerpenguins’

The following object is masked from ‘package:modeldata’:

    penguins

Day 3 Learning Objectives#

Compute the Euclidean distance between points on a graph
Implement the K-nearest neighbours classification algorithm
Describe the importance of a training and test set in machine learning
Explain the use and importance of cross-validation
Compare and contrast a variety of performance metrics
Execute the K-nearest neighbours regression algorithm
Understand the difference between regression and classification

1. Classification#

Machine learning is a field where computers learn from data and make decisions and predictions. Classification is a type of machine learning, where the goal is to predict a categorical class of an observation given other variables (features). For example:

Classifying an email as “spam” or “not spam”
Classifying a medical test as “positive” or “negative”
Classifying a bank transaction as fraudulent or not

Suppose we have past data of cancer tumour cell diagnosis labelled “benign” and “malignant”. Do you think a new cell with Concavity = 3.3 and Perimeter = 0.2 would be malignant? How did you decide?

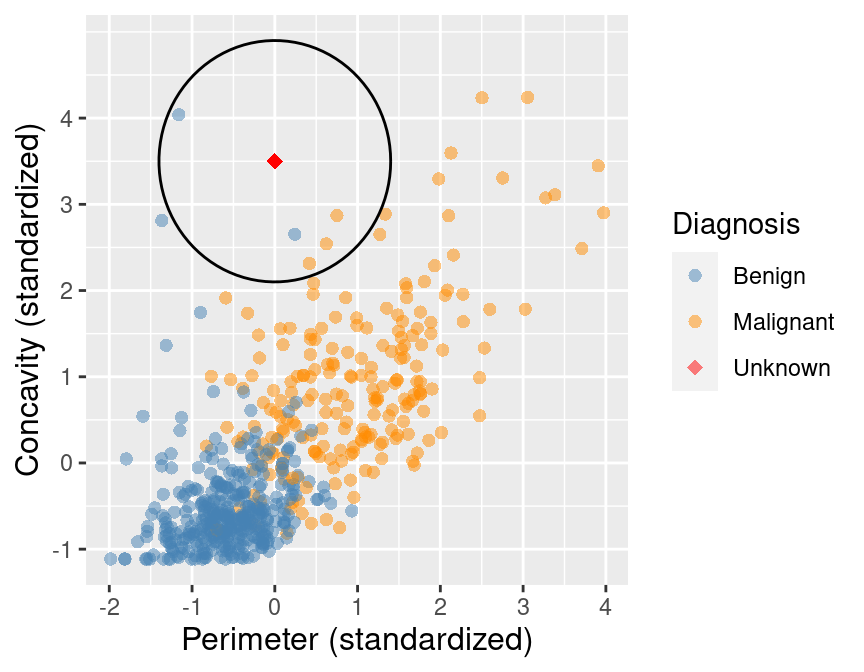
What kind of data analysis question is this?#

Descriptive, exploratory, predictive, inferential, causal, or mechanistic?

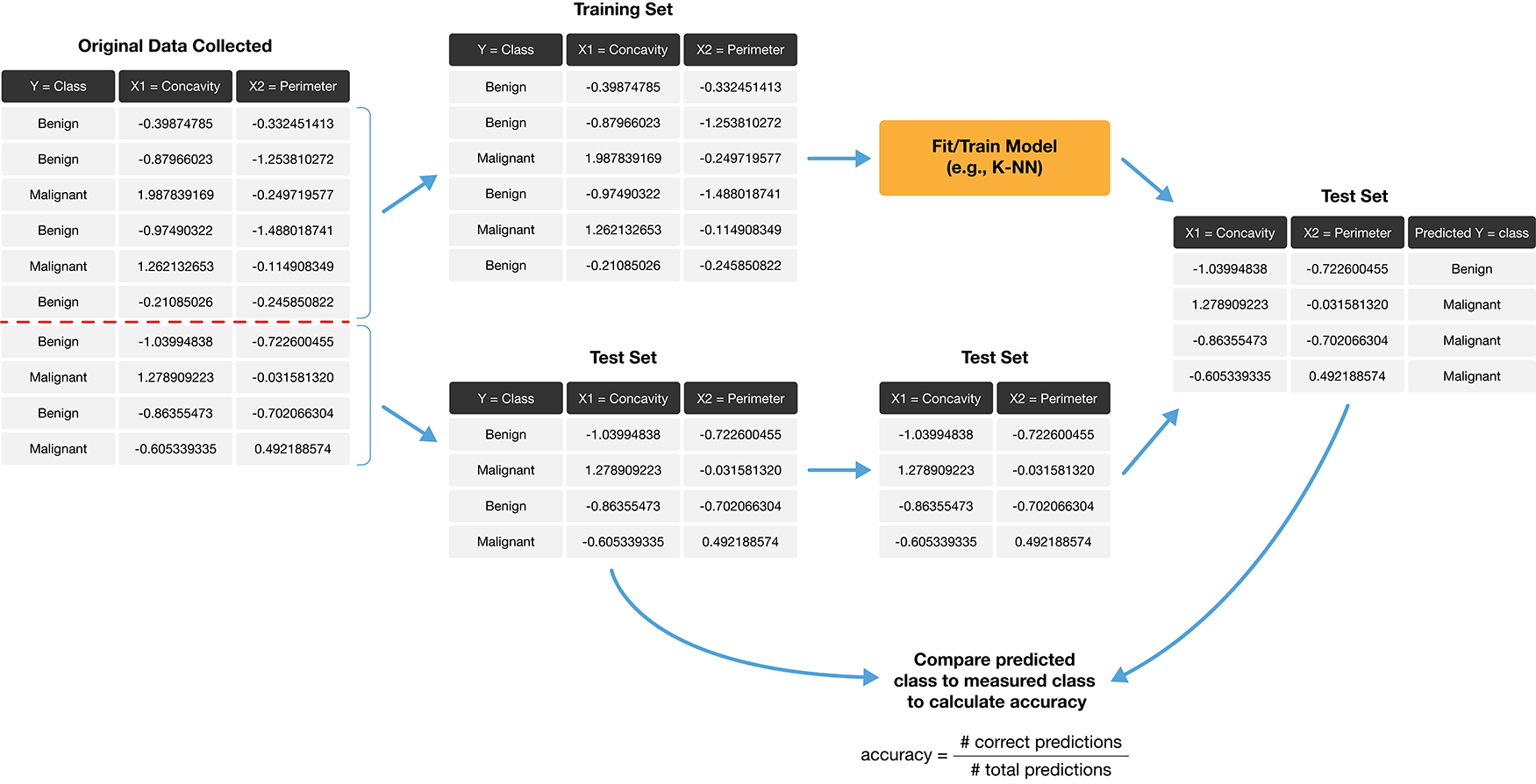
1.2 Training and Test Sets#

When building a machine learning model, typically we start by dividing our data into two sets:

Training set
Test set

The training set is a subset of our data that is used is to train or teach our model to perform sort of predictive task. Then, using our test set, we can evaluate how well our model performs on unseen data.

There are two important things to do when splitting data.

Shuffling: randomly reorder the data before splitting
Stratification: make sure the two split subsets of data have roughly equal proportions of the different labels

Golden Rule of Machine Learning / Statistics:#

Don’t use your testing data to train your model!

Showing your classifier the labels of evaluation data is like cheating on a test; it’ll look more accurate than it really is.

1.3 K-nearest neighbours classification#

Predict the label / class for a new observation using the K closest points from our dataset.

Compute the distance between the new observation and each observation in our training set

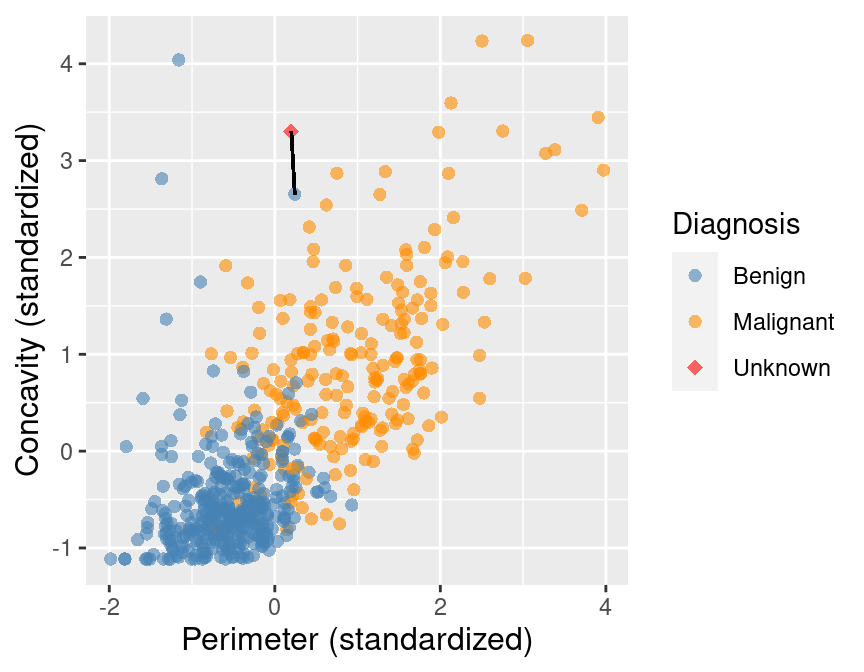
$\text{Distance} = \sqrt{(x_{\text{new}} - x_{\text{train}})^2 + (y_{\text{new}} - y_{\text{train}})^2}$

The new point is at perimeter $= 0.2$, concavity $= 3.3$
Recall that the training dataset is the sample of data used to fit the model.
Suppose we have a set of data and we want to predict the class of a new observation. We first want to calculate the distance between the new observation and the other points and predict the label / class for a new observation using the $K$ closest points from our dataset.

Sort the data in ascending order according to the distances
Choose the top K rows as “neighbours”

## # A tibble: 5 x 5
##        ID Perimeter Concavity Class dist_from_new
##     <dbl>     <dbl>     <dbl> <fct>         <dbl>
## 1   86409     0.241      2.65 B             0.881
## 2  887181     0.750      2.87 M             0.980
## 3  899667     0.623      2.54 M             1.14 
## 4  907914     0.417      2.31 M             1.26 
## 5 8710441    -1.16       4.04 B             1.28

Classify the new observation based on majority vote.

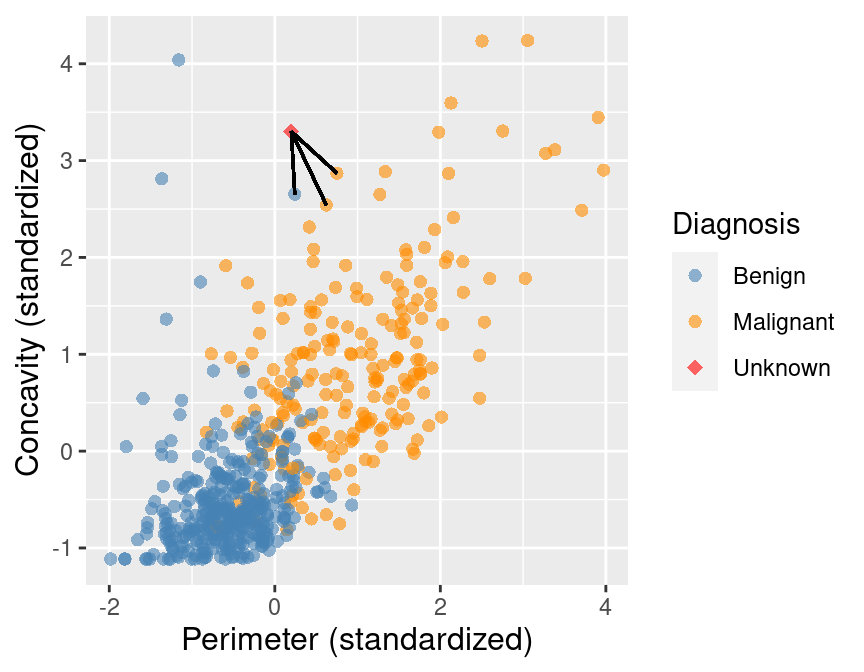
What would the predicted class be?#

We can go beyond 2 predictors!#

For two observations $u, v$, each with $m$ variables (columns) labelled $1, \dots, m$,

$\text{Distance} = \sqrt{(u_1-v_1)^2 + (u_2-v_2)^2 + \dots + (u_m - v_m)^2}$

Aside from that, it’s the same algorithm!

1.4 Standardizing Data#

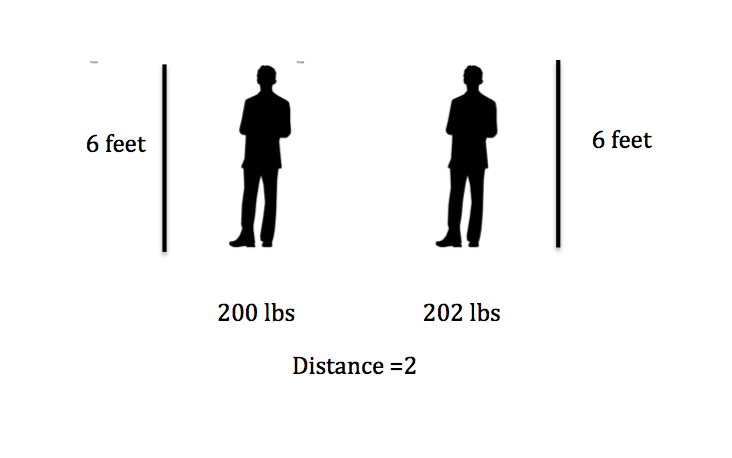
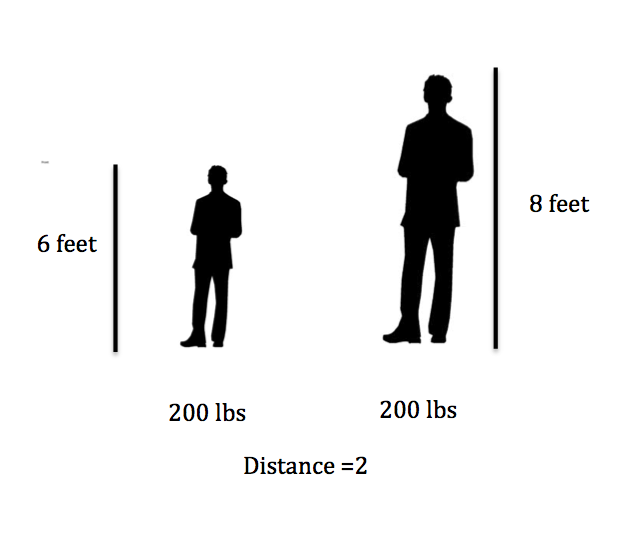
When using K-nearest neighbour classification, the scale of each variable (i.e., its size and range of values) matters. e.g. Salary (10,000+) and Age (0-100)
Since the classifier predicts classes by identifying observations that are nearest to it, any variables that have a large scale will have a much larger effect than variables with a small scale.
But just because a variable has a large scale doesn’t mean that it is more important for making accurate predictions.
For example, suppose you have a data set with two attributes, height (in feet) and weight (in pounds).

distance1 = sqrt((202 - 200)^2 + (6 - 6)^2) = 2

distance2 = sqrt((200 - 200)^2 + (8 - 6)^2) = 2

Here if we calculate the distance we get 2 in both cases! A difference of 2 pounds is not that big, but a different in 2 feet is a lot. So how can we adjust for this?

Nonstandardized Data vs. Standardized Data#

What if one variable is much larger than the other?

Standardize: shift and scale so that the average is 0 and the standard deviation is 1.

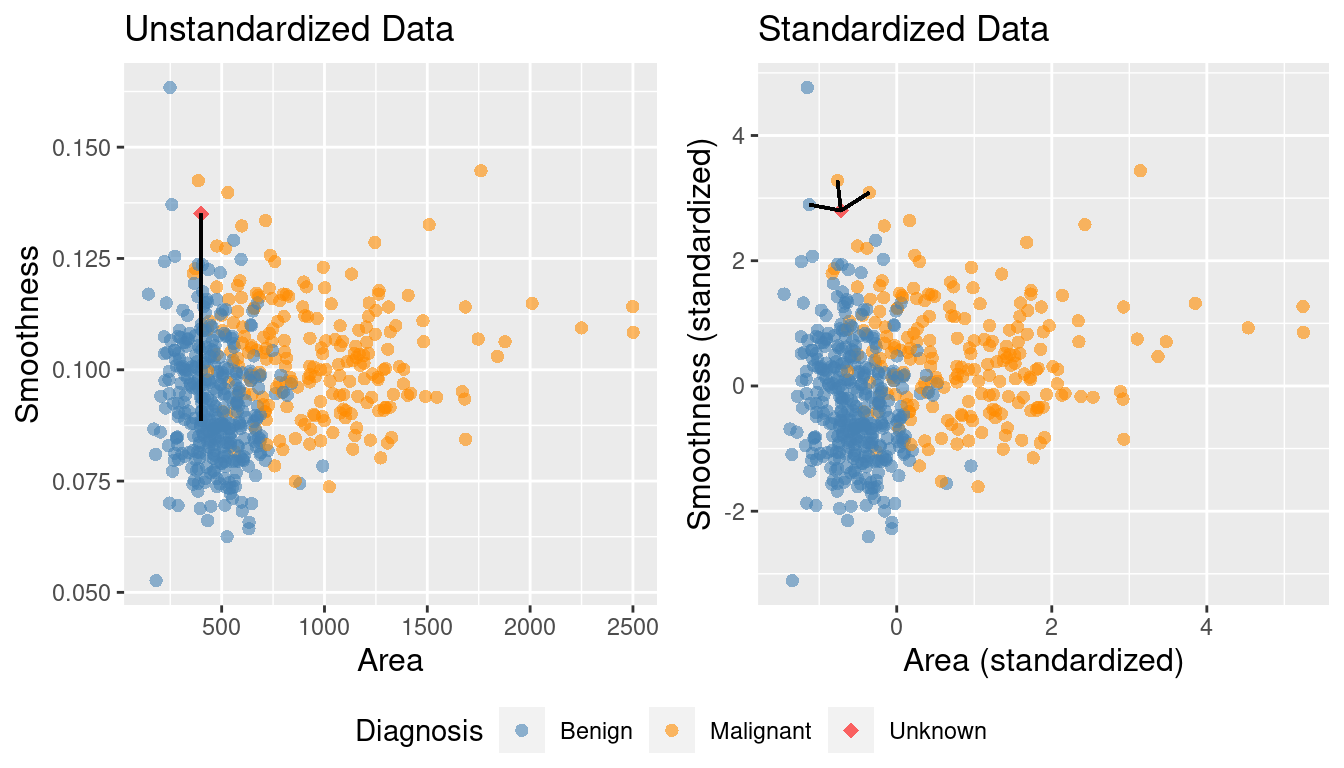
Standardization: when all variables in a data set have a mean (center) of 0 and a standard deviation (scale) of 1, we say that the data have been standardized.

In the plot with the original data above, its very clear that K-nearest neighbours would classify the red dot (new observation) as malignant. However, once we standardize the data, the diagnosis class labelling becomes less clear, and appears it would depend upon the choice of
$K$.
Thus, standardizing the data can change things in an important way when we are using predictive algorithms. As a rule of thumb, standardizing your data should be a part of the preprocessing you do before any predictive modelling / analysis.

1.5 `tidymodels` package in R#

tidymodels is a collection of packages and handles computing distances, standardization, balancing, and prediction for us!

Source: https://www.r-bloggers.com/2019/06/a-gentle-introduction-to-tidymodels/

# Data on cancer tumors
tumors <- read_csv("data/clean-wdbc.data.csv") |>
    mutate(Class = as_factor(Class))

head(tumors)

Rows: 569 Columns: 12

── Column specification ───────────────────────────────────────────────────────────────────────────────────
Delimiter: ","
chr  (1): Class
dbl (11): ID, Radius, Texture, Perimeter, Area, Smoothness, Compactness, Con...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

A tibble: 6 × 12
ID	Class	Radius	Texture	Perimeter	Area	Smoothness	Compactness	Concavity	Concave_points	Symmetry	Fractal_dimension
<dbl>	<fct>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
842302	M	1.8850310	-1.35809849	2.3015755	1.9994782	1.3065367	2.6143647	2.1076718	2.2940576	2.7482041	1.9353117
842517	M	1.8043398	-0.36887865	1.5337764	1.8888270	-0.3752817	-0.4300658	-0.1466200	1.0861286	-0.2436753	0.2809428
84300903	M	1.5105411	-0.02395331	1.3462906	1.4550043	0.5269438	1.0819801	0.8542223	1.9532817	1.1512420	0.2012142
84348301	M	-0.2812170	0.13386631	-0.2497196	-0.5495377	3.3912907	3.8899747	1.9878392	2.1738732	6.0407261	4.9306719
84358402	M	1.2974336	-1.46548091	1.3373627	1.2196511	0.2203623	-0.3131190	0.6126397	0.7286181	-0.8675896	-0.3967505
843786	M	-0.1653528	-0.31356043	-0.1149083	-0.2441054	2.0467119	1.7201029	1.2621327	0.9050914	1.7525273	2.2398308

In tidymodels, the recipes package is named after cooking terms.

1. Make a `recipe` to specify the predictors/response and preprocess the data#

recipe(): Main argument in the formula.

Arguments:
- formula
- data
prep() & bake(): you can also prep and bake a recipe to see what the preprocessing does!

The prep() function computes everything so that the preprocessing steps can be executed
The bake() function takes a recipe and applies it to data and returns data
visit https://recipes.tidymodels.org/reference/index.html to see all the preprocessing steps

# Standardize the data

tumor_recipe <- recipe(Class ~ Perimeter + Concavity, data=tumors) |>
                  step_center(all_predictors()) |>
                  step_scale(all_predictors()) 
tumor_recipe           

── Recipe ─────────────────────────────────────────────────────────────────────────────────────────────────

── Inputs

Number of variables by role

outcome:   1
predictor: 2

── Operations

• Centering for: all_predictors()

• Scaling for: all_predictors()

2. Build a model specification (`model_spec`) to specify the model and training algorithm#

model type: kind of model you want to fit
arguments: model parameter values
engine: underlying package the model should come from
mode: type of prediction (some packages can do both classification and regression)

# Build a model specification using nearest_neighbor

tumor_model <- nearest_neighbor(weight_func = "rectangular", neighbors = 3) |>
       set_engine("kknn") |>
       set_mode("classification")

tumor_model

K-Nearest Neighbor Model Specification (classification)

Main Arguments:
  neighbors = 3
  weight_func = rectangular

Computational engine: kknn 

3. Put them together in a workflow and then `fit` it#

We may want to use our recipe across several steps as we train and test our model. To simplify this process, we can use a model workflow, which pairs a model and recipe together.

# Create a workflow

tumor_workflow <- workflow() |>
    add_recipe(tumor_recipe) |>
    add_model(tumor_model)

tumor_fit <- tumor_workflow |>
    fit(data=tumors)

tumor_workflow

══ Workflow ═══════════════════════════════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: nearest_neighbor()

── Preprocessor ───────────────────────────────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_center()
• step_scale()

── Model ──────────────────────────────────────────────────────────────────────────────────────────────────
K-Nearest Neighbor Model Specification (classification)

Main Arguments:
  neighbors = 3
  weight_func = rectangular

Computational engine: kknn 

4. Predict a new class label using `predict`#

predict() applies the recipe to the new data, then passes them to the fitted model.

new_obs <- tibble(Perimeter = 0.2, Concavity = 3.3)

predict(tumor_fit, new_obs)

A tibble: 1 × 1
.pred_class
<fct>
M

What would happen to the prediction if we changed Perimeter to -2?

1.6 How to measure classifier performance?#

Accuracy#

\[Accuracy = \dfrac{\#\; correct\; predictions}{\#\; total\; predictions}\]

Downside: doesn’t tell you the type of mistake being made

Here is an example of confusion matrix with cancer diagnosis data we’ve seen before.

	Truly Malignant	Truly Benign
Predicted Malignant	1	4
Predicted Benign	3	57

Typically we consider one of the class labels as “positive” - in this case the “Malignant” status is more interesting to researchers, hence we consider that label as “positive”.

Relabeling the above confusion matrix:

	Truly Positive	Truly Negative
Predicted Positive	1	4
Predicted Negative	3	57

Note that:

Top left cell = # correct positive predictions.
Top row = # total positive predictions.
Left column = # truly positive observations.

Precision and Recall#

\[ {Precision} = \dfrac{{\#\; correct\; positive\; predictions}}{{\#\; total\; positive\; predictions}} \quad\quad\quad \quad {Recall} = \dfrac{{\#\; correct\; positive\; predictions}}{{\#\; total\; truly\; positive\; observations}} \]

In the above confusion matrix, precision = 1/(1+4) and recall = 1/(1+3).

Precision quantifies how many of the positive predictions the classifier made were actually positive. Intuitively, we would like a classifier to have a high precision: for a classifier with high precision, if the classifier reports that a new observation is positive, we can trust that the new observation is indeed positive.

Recall quantifies how many of the positive observations in the test set were identified as positive. Intuitively, we would like a classifier to have a high recall: for a classifier with high recall, if there is a positive observation in the test data, we can trust that the classifier will find it.

In-class Question#

a 99% accuracy on cancer prediction may not be very useful. Why?
If we need patients with truly malignant cancer to be diagnosed correctly, what metric should we prioritize?
What if a classifier never guess positive except for the very few observations it is super confident in? What metric is affected?

To add evaluation into our classification pipeline, we:

i.) Split our data into two subsets: training data and testing data (discussed above).

ii.) Build the model & choose K using training data only (sometimes called tuning)

iii.) Compute performance metrics (accuracy, precision, recall, etc.) by predicting labels on testing data only

We’ll now talk about these steps below.

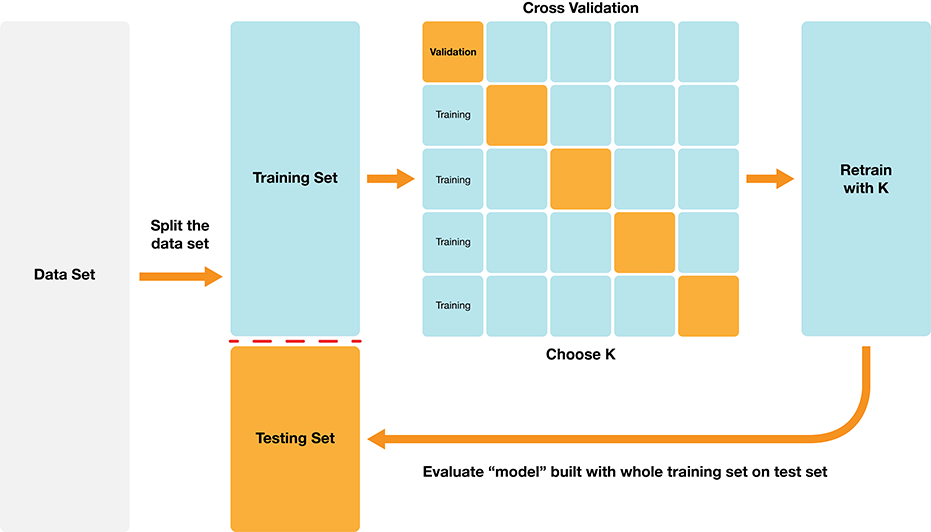
1.7 Choosing K (or, “tuning’’ the model)#

Choosing K is part of training. We want to choose K to maximize performance, but:

we can’t use test data to evaluate performance (cheating!)
we can’t use training data to evaluate performance (that’s what we trained with, so poor evaluation of true performance)

Solution: Split the training data further into training data and validation data sets

a. Choose some candidate values of K
b. Split the training data into two sets - one called the training set, another called the validation set
c. For each K, train the model using training set only
d. Evaluate accuracy (and/or other metrics of performance) for each using validation set only
e. Pick the K that maximizes validation performance

But what if we get a bad training set? Just by chance?

Cross-Validation#

We can get a better estimate of performance by splitting multiple ways and averaging. Here’s an example:

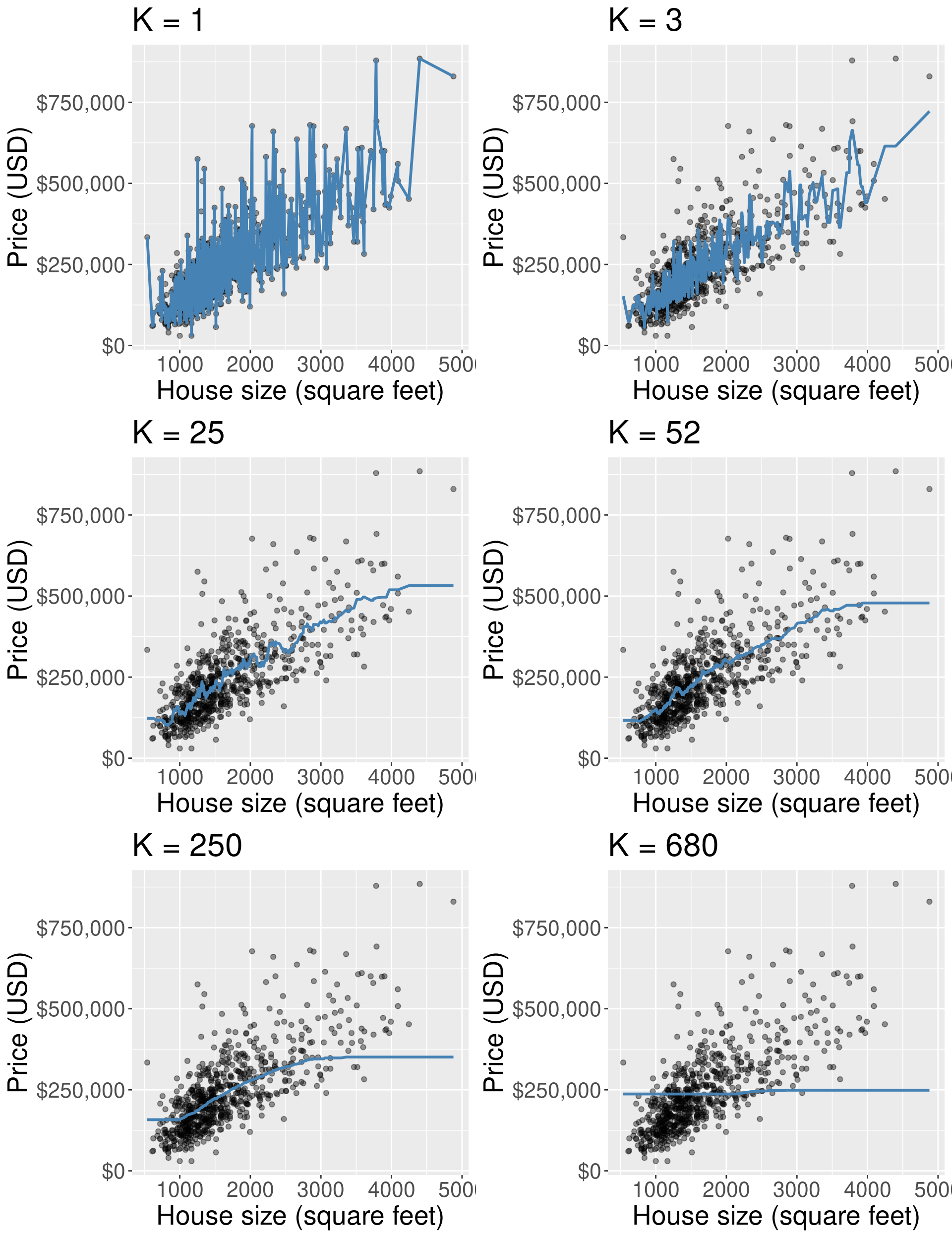
Underfitting & Overfitting#

Overfitting: when your model is too sensitive to your training data; noise can influence predictions!

Underfitting: when your model isn’t sensitive enough to training data; useful information is ignored!

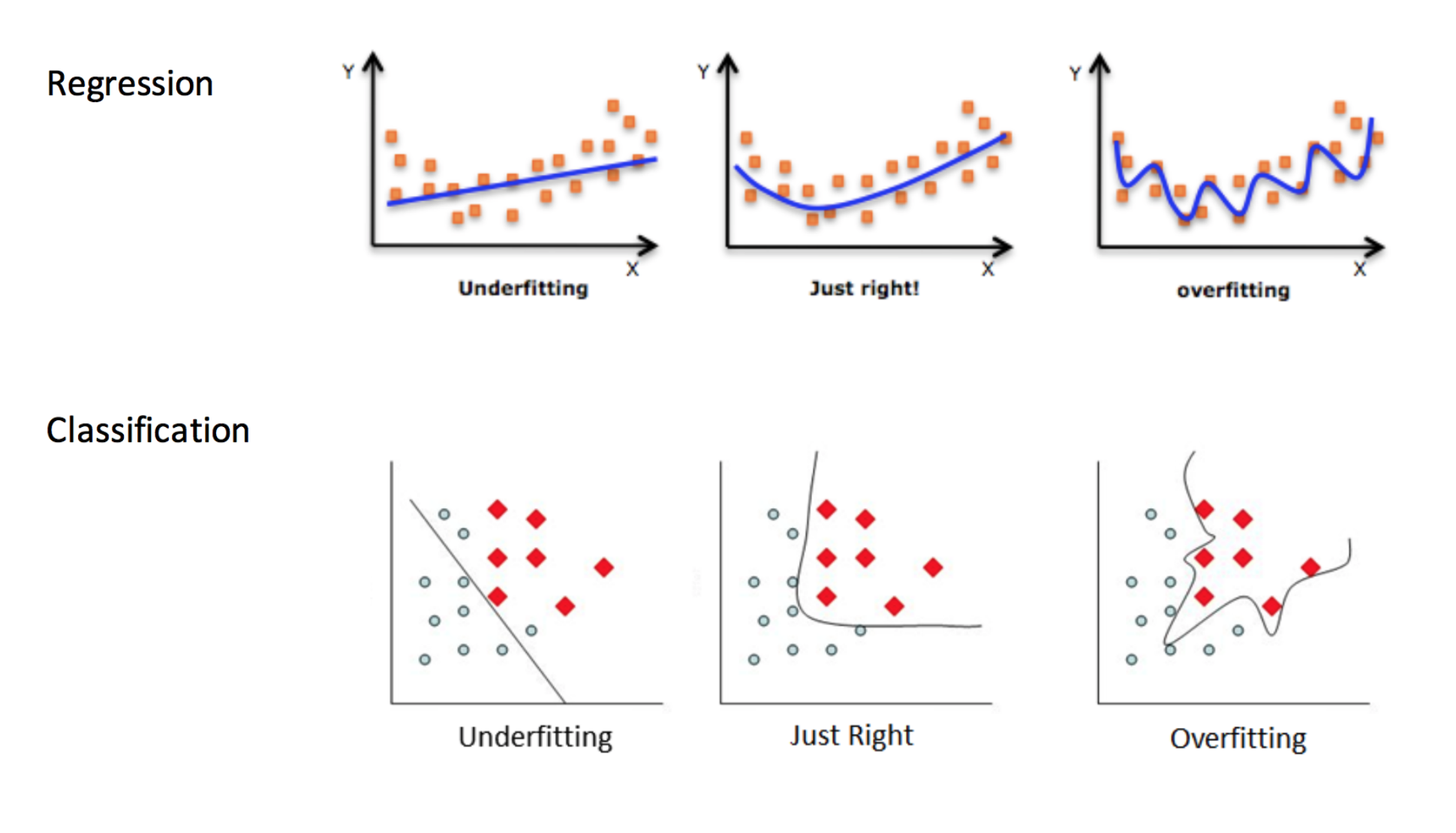
Source: http://kerckhoffs.schaathun.net/FPIA/Slides/09OF.pdf

Underfitting & Overfitting#

Which of these are under-, over-, and good fits?

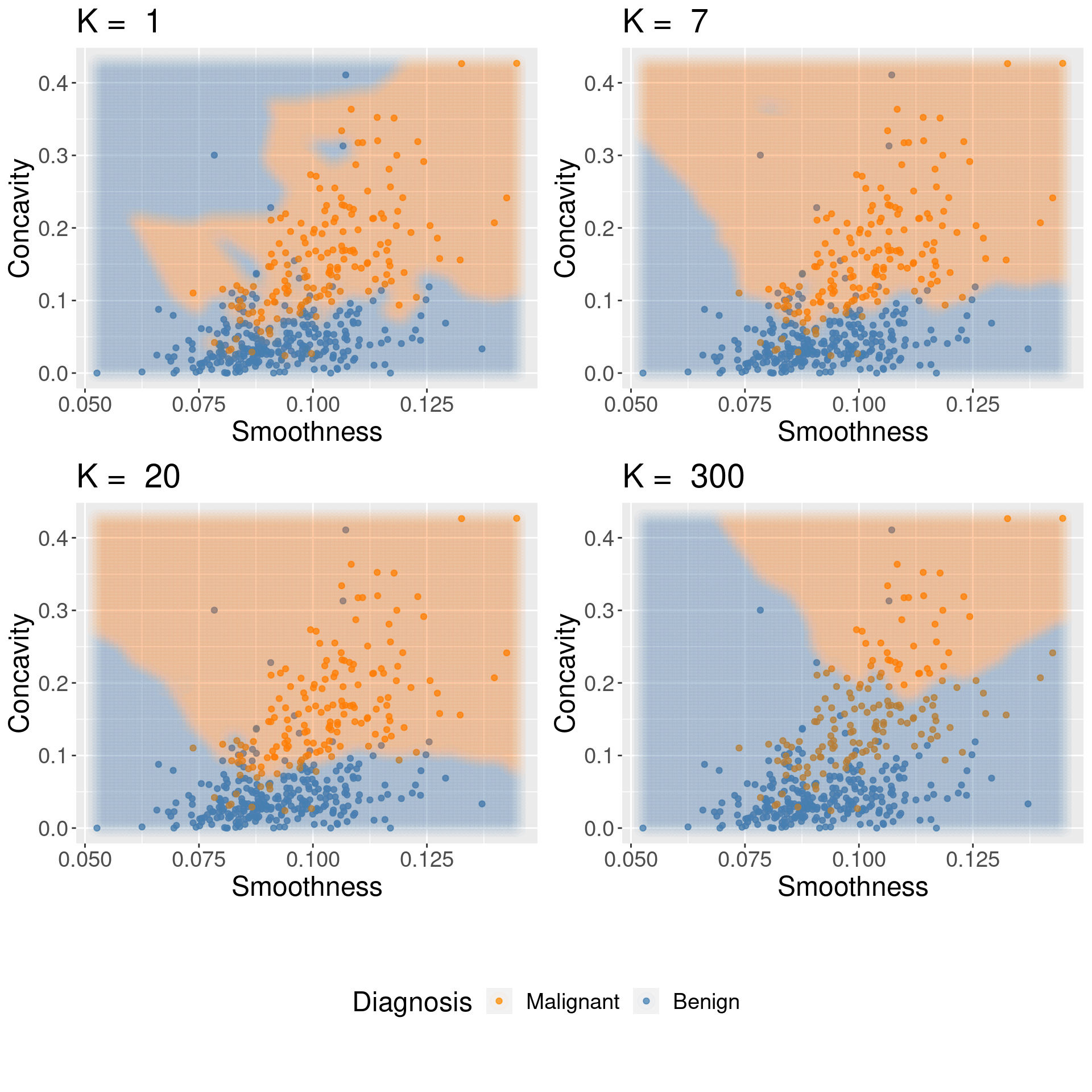
Underfitting & Overfitting#

For KNN: small K overfits, large K underfits, both result in lower accuracy

1.8 Compute performance metrics#

The role of the test data:

The Big Picture#

Now, let’s put it all together and look into how to go about this process in R. First let’s split our data into training and test sets:

# Split data

set.seed(1) # set seed for reproducibility

tumor_split <- initial_split(tumors, prop = 0.75, strata = Class)
tumor_train <- training(tumor_split) # training set 
tumor_test <- testing(tumor_split) # testing set 

What is the proportion of malignant tumors in our training set?

tumor_proportions <- tumor_train |>
                      group_by(Class) |>
                      summarize(n = n()) |>
                      mutate(percent = 100*n/nrow(tumor_train))

tumor_proportions

A tibble: 2 × 3
Class	n	percent
<fct>	<int>	<dbl>
M	159	37.32394
B	267	62.67606

Standardize the training data:

tumor_recipe <- recipe(Class ~ Smoothness + Concavity, data = tumor_train) |>
  step_scale(all_predictors()) |>
  step_center(all_predictors())

Instead of specifying $K$ in our model specification, we can set neighbors = tune() to later select the optimal $K$ using cross-validation.

tumor_model <- nearest_neighbor(weight_func = "rectangular",
                              neighbors = tune()) |>
                  set_engine("kknn") |>
                  set_mode("classification")

After, we can use the tune_grid function in our workflow for a range of potential values for $K$ and fit the model with the training data.

tumor_vfold <- vfold_cv(tumor_train, v = 5, strata = Class)

k_vals <- tibble(neighbors = seq(from = 1, to = 100, by = 5))

knn_fit <- workflow() |>
  add_recipe(tumor_recipe) |>
  add_model(tumor_model)|>
  tune_grid(resamples = tumor_vfold, grid = k_vals) |>
  collect_metrics()

accuracies <- knn_fit |>
  filter(.metric == "accuracy")

head(accuracies)

A tibble: 6 × 7
neighbors	.metric	.estimator	mean	n	std_err	.config
<dbl>	<chr>	<chr>	<dbl>	<int>	<dbl>	<chr>
1	accuracy	binary	0.7840636	5	0.016340207	Preprocessor1_Model01
6	accuracy	binary	0.8403746	5	0.006980546	Preprocessor1_Model02
11	accuracy	binary	0.8310175	5	0.007745668	Preprocessor1_Model03
16	accuracy	binary	0.8451918	5	0.014306532	Preprocessor1_Model04
21	accuracy	binary	0.8663155	5	0.019746677	Preprocessor1_Model05
26	accuracy	binary	0.8569025	5	0.020014323	Preprocessor1_Model06

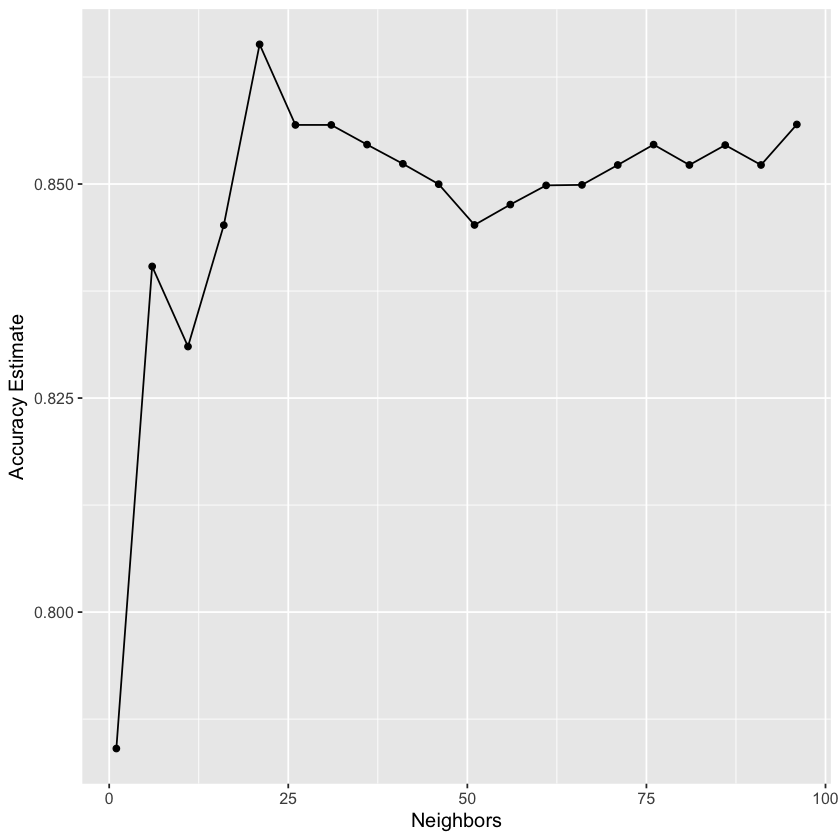
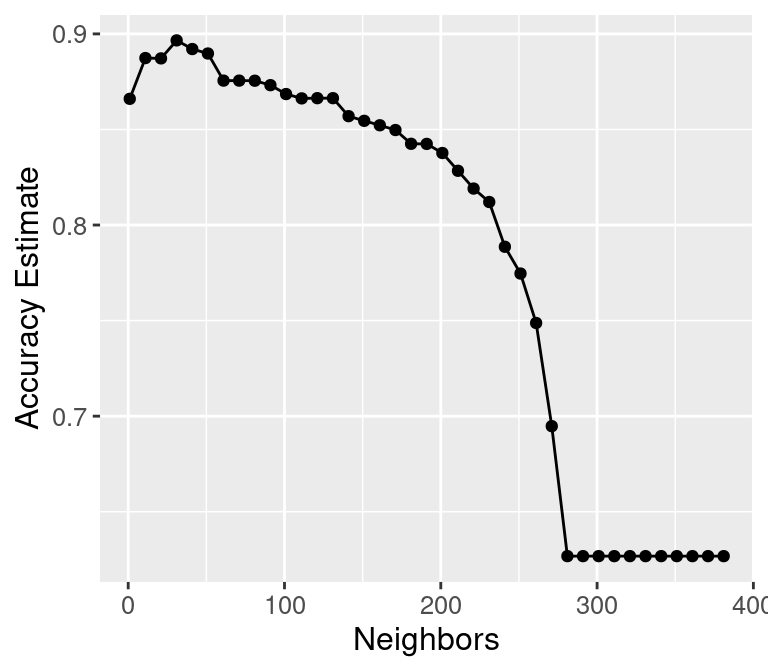
accuracy_vs_k <- ggplot(accuracies, aes(x = neighbors, y = mean)) +
  geom_point() +
  geom_line() +
  labs(x = "Neighbors", y = "Accuracy Estimate") +
  theme(text = element_text(size = 12))

accuracy_vs_k

../_images/aaa5a6e733b40594e9a46eceaf7ac88464fa407f6984dd99f91365ba7ab21d74.png

best_k <- accuracies |>
        arrange(desc(mean)) |>
        head(1) |>
        pull(neighbors)
best_k

21

Let’s fit our model with our “best” $K$ value.

Note: In the worksheet, we will provide you with a $K$ value to use and you won’t need to perform cross-validation, but it is still good to understand the motivation behind it!

tumor_model <- nearest_neighbor(weight_func = "rectangular", neighbors = best_k) |>
  set_engine("kknn") |>
  set_mode("classification")

tumor_fit <- workflow() |>
  add_recipe(tumor_recipe) |>
  add_model(tumor_model) |>
  fit(data = tumor_train)

tumor_fit

══ Workflow [trained] ═════════════════════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: nearest_neighbor()

── Preprocessor ───────────────────────────────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_scale()
• step_center()

── Model ──────────────────────────────────────────────────────────────────────────────────────────────────

Call:
kknn::train.kknn(formula = ..y ~ ., data = data, ks = min_rows(21,     data, 5), kernel = ~"rectangular")

Type of response variable: nominal
Minimal misclassification: 0.1384977
Best kernel: rectangular
Best k: 21

Now, we can make predictions on our test set!

tumor_test_predictions <- predict(tumor_fit, tumor_test) |>
  bind_cols(tumor_test)

head(tumor_test_predictions)

A tibble: 6 × 13
.pred_class	ID	Class	Radius	Texture	Perimeter	Area	Smoothness	Compactness	Concavity	Concave_points	Symmetry	Fractal_dimension
<fct>	<dbl>	<fct>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
M	84501001	M	-0.2439749	2.4409613	-0.2860264	-0.297147713	2.3182555	5.1083824	3.991920	1.61859101	2.3683599	6.8408368
B	846381	M	0.1181009	0.3225990	0.1410247	-0.007171473	-0.8439134	-0.3932021	-0.191677	-0.04117035	-0.1483101	-1.1669069
M	84799002	M	0.2463792	1.8633740	0.5011165	0.109978225	1.5518018	2.5641538	2.063094	0.86097309	2.1291389	2.7768917
M	849014	M	2.2864179	0.8464951	2.3670467	2.665141363	0.8247658	0.3860195	1.270281	1.88938618	-0.2145808	-0.4316318
M	852763	M	0.2794833	1.2255875	0.4505251	0.028658420	0.8817023	2.6061021	1.350329	2.36555969	2.2034913	2.4114688
M	853401	M	1.4236429	1.3557481	1.5843678	1.386505974	0.7327913	1.0896071	1.635052	1.06787276	0.8780775	0.7681733

Finally, we can look at evaluation measures for our model such as accuracy.

tumor_test_predictions |>
  metrics(truth = Class, estimate = .pred_class) |>
  filter(.metric == "accuracy")

A tibble: 1 × 3
.metric	.estimator	.estimate
<chr>	<chr>	<dbl>
accuracy	binary	0.8671329

Take a look at the confusion matrix below. Using the table, verify that the accuracy was computed correctly.

confusion <- tumor_test_predictions |>
             conf_mat(truth = Class, estimate = .pred_class)
confusion

          Truth
Prediction  M  B
         M 42  8
         B 11 82

Question#

What are the precision and recall for the classifier on the test data?

We can use the precision and recall functions from tidymodels.

tumor_test_predictions |>
  precision(truth = Class, estimate = .pred_class, event_level = "first")

A tibble: 1 × 3
.metric	.estimator	.estimate
<chr>	<chr>	<dbl>
precision	binary	0.84

tumor_test_predictions |>
  recall(truth = Class, estimate = .pred_class, event_level = "first")

A tibble: 1 × 3
.metric	.estimator	.estimate
<chr>	<chr>	<dbl>
recall	binary	0.7924528

Activity#

In a group, discuss the following prompts.

Explain what a test and training data set are in your own words
Explain cross-validation in your own words
Imagine if we train and evaluate accuracy on all the data. How can I get 100% accuracy, always?

2. Regression#

What if we want to predict a quantitative value instead of a class label? Say, the sale price of a home.

# Read in the data

housing <- read_csv("data/housing.csv")

head(housing)

Rows: 932 Columns: 9

── Column specification ───────────────────────────────────────────────────────────────────────────────────
Delimiter: ","
chr (3): city, zip, type
dbl (6): beds, baths, sqft, price, latitude, longitude

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

A tibble: 6 × 9
city	zip	beds	baths	sqft	type	price	latitude	longitude
<chr>	<chr>	<dbl>	<dbl>	<dbl>	<chr>	<dbl>	<dbl>	<dbl>
SACRAMENTO	z95838	2	1	836	Residential	59222	38.63191	-121.4349
SACRAMENTO	z95823	3	1	1167	Residential	68212	38.47890	-121.4310
SACRAMENTO	z95815	2	1	796	Residential	68880	38.61830	-121.4438
SACRAMENTO	z95815	2	1	852	Residential	69307	38.61684	-121.4391
SACRAMENTO	z95824	2	1	797	Residential	81900	38.51947	-121.4358
SACRAMENTO	z95841	3	1	1122	Condo	89921	38.66260	-121.3278

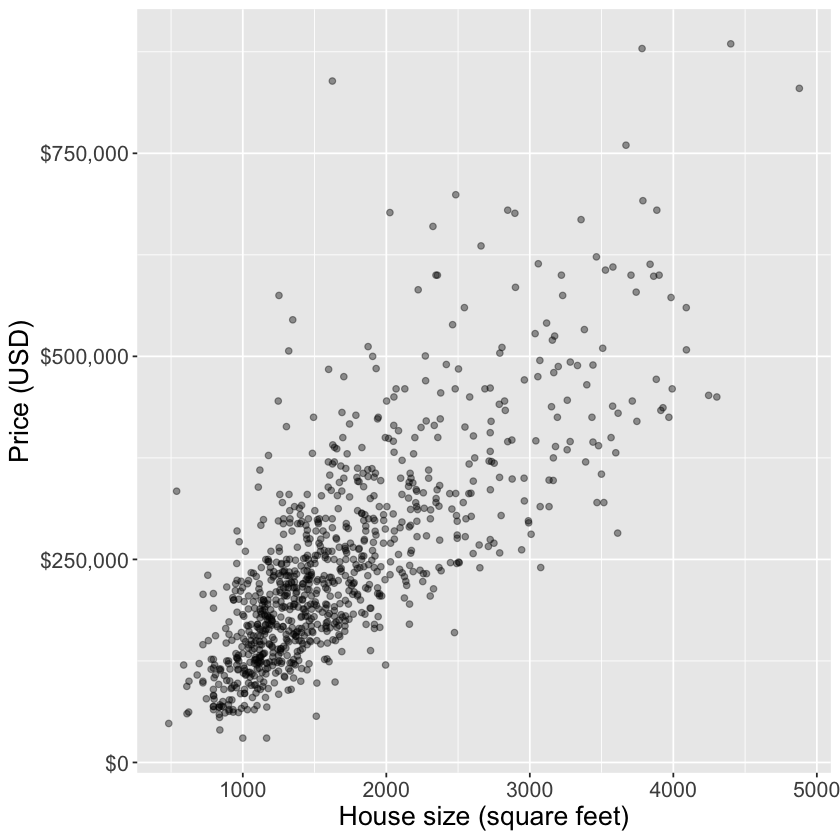
ggplot(housing, aes(x = sqft, y = price)) +
  geom_point(alpha = 0.4) +
  xlab("House size (square feet)") +
  ylab("Price (USD)") +
  scale_y_continuous(labels = dollar_format()) +
  theme(text = element_text(size = 16))

../_images/07a74448a5175b75d7283fff74c34c564a1ccba5290c67baf8b893cb6fa60fae.png

E.g.: predict the price of a 2000 square foot home (from this reduced dataset)

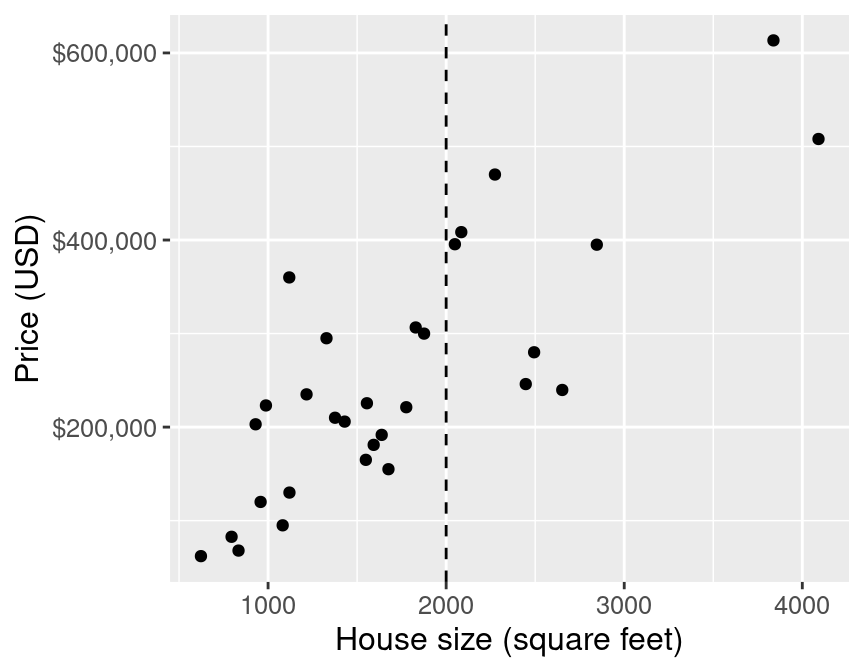
https://datasciencebook.ca/_main_files/figure-html/07-small-eda-regr-1.png

You can see that we have no observations of a house of size exactly 2,000 square feet
- What are some ways you might predict the price?

2.1 K nearest neighbours regression#

As in k-nn classification, we find the $k$-nearest neighbours (here $k=5$) in terms of the predictors

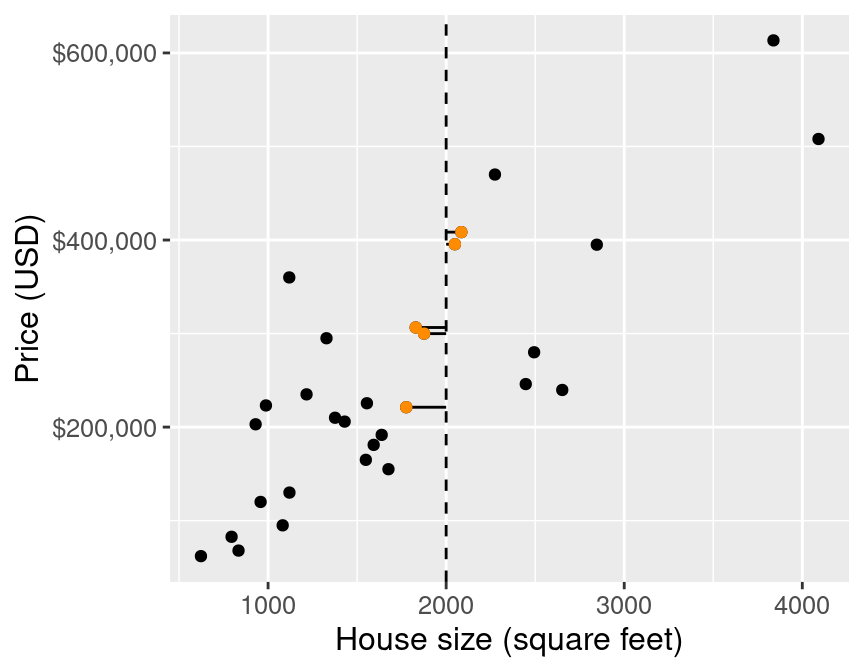
https://datasciencebook.ca/_main_files/figure-html/07-knn3-example-1.png

Then we average the values for the $k$-nearest neighbours, and use that as the prediction:

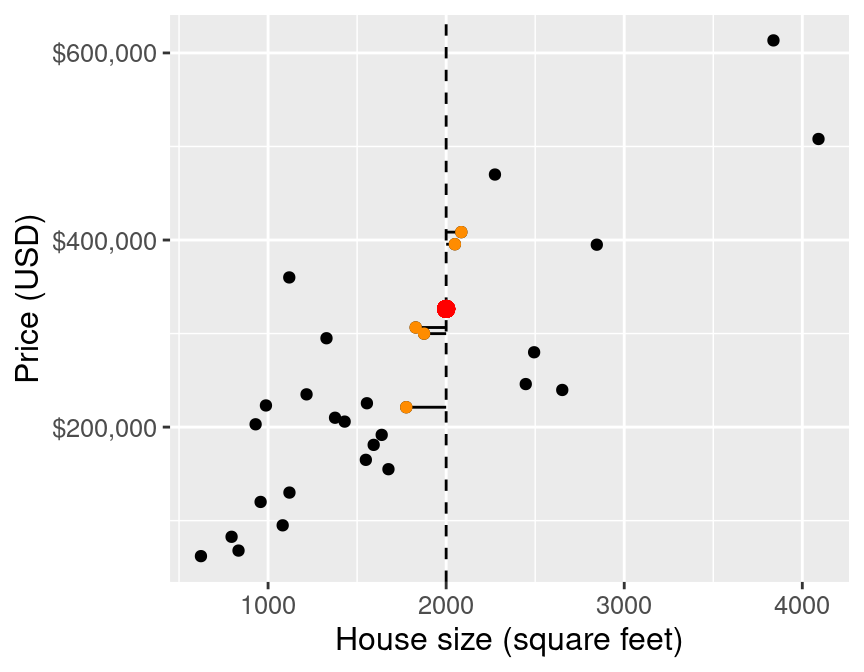
https://datasciencebook.ca/_main_files/figure-html/07-predictedViz-knn-1.png

If we do that for a range of house sizes, we can draw the curve of predictions:

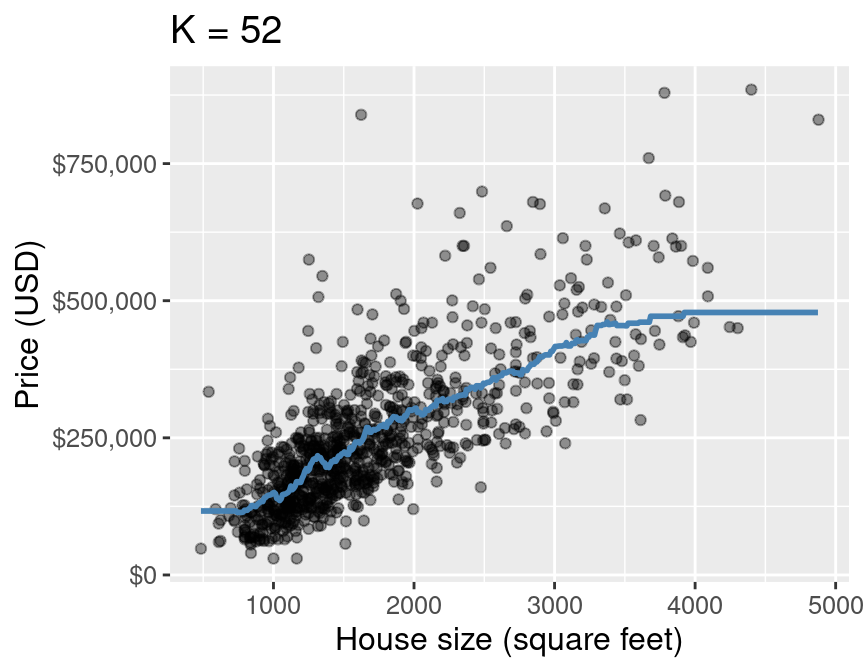
https://datasciencebook.ca/_main_files/figure-html/07-predict-all-1.png

You can imagine doing this for all the possible input values and coming up with predictions everywhere
Connecting all these predictions with a line
one benefit is that it handles non-linearity well.

2.2 Model Evaluation and Tuning#

We still have to answer these two questions:

Is our model any good?
How do we choose k?

The same general strategy as in classification works here!

https://datasciencebook.ca/img/classification2/train-test-overview.png

Is our model any good?#

The blue line depicts our predictions from k-nn regression. The red lines depict the error in our predictions, i.e., the difference between the $i^\text{th}$ test data response and our prediction $\hat{y}_i$:

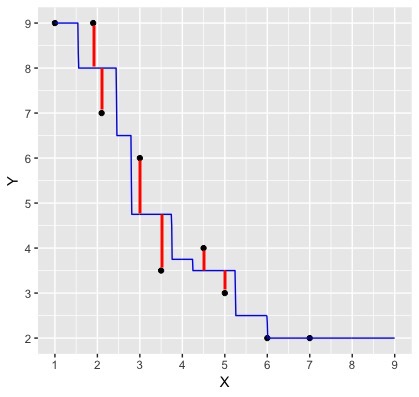
We now have the errors for individual points. How could you combine these errors to report a single measure of error for our model?

We (roughly) add up these errors to evaluate our regression model

Not out of 1, but instead in units of the target variable (bit harder to interpret)

Root Mean Squared Prediction Error (RMSPE):

\[RMSPE = \sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(y_i - \hat{y_i})^2}\]

- $n$ is the number of observations

- $y_i$ is the observed value for the $i^\text{th}$ test observation

- $\hat{y_i}$ is the predicted value for the $i^\text{th}$ test observation

We choose $K$ roughly the same way as before:

Cross validation:
- Split data into $C$ folds
- Train
- Evaluate model
- Pick k that gives the lowest RMSPE on validation set
Train model on whole training dataset (not split into folds)
Evaluate how good the predictions are using the test data

The process is very similar to what we learned for classification, except for a few minor changes to our model:

# Split the data

set.seed(123)

housing_split <- initial_split(housing, prop = 0.75, strata = price)
housing_train <- training(housing_split)
housing_test <- testing(housing_split)

# Standardize the training data

housing_recipe <- recipe(price ~ sqft, data = housing_train) |>
  step_scale(all_predictors()) |>
  step_center(all_predictors())

# Specify the regression model 

housing_model <- nearest_neighbor(weight_func = "rectangular",
                              neighbors = tune()) |>
  set_engine("kknn") |>
  set_mode("regression") # Note we change this to regression instead of classification

# Set the folds for cross validation

housing_vfold <- vfold_cv(housing_train, v = 5, strata = price)

# Define our workflow 

housing_wkflw <- workflow() |>
  add_recipe(housing_recipe) |>
  add_model(housing_model)

housing_wkflw

══ Workflow ═══════════════════════════════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: nearest_neighbor()

── Preprocessor ───────────────────────────────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_scale()
• step_center()

── Model ──────────────────────────────────────────────────────────────────────────────────────────────────
K-Nearest Neighbor Model Specification (regression)

Main Arguments:
  neighbors = tune()
  weight_func = rectangular

Computational engine: kknn 

Using cross-validation, we search a grid of potential values for $K$ between 1 and 200:

gridvals <- tibble(neighbors = seq(from = 1, to = 200, by = 3))

housing_results <- housing_wkflw |>
  tune_grid(resamples = housing_vfold, grid = gridvals) |>
  collect_metrics() |>
  filter(.metric == "rmse")

# show only the row of minimum RMSPE
housing_min <- housing_results |>
  filter(mean == min(mean))

housing_min

A tibble: 1 × 7
neighbors	.metric	.estimator	mean	n	std_err	.config
<dbl>	<chr>	<chr>	<dbl>	<int>	<dbl>	<chr>
52	rmse	standard	86615.41	5	5486.112	Preprocessor1_Model18

It looks like $K=52$ gives us the lowest RMSE! Now, let’s evaluate how our model performs on unseen testing data using RMSPE:

kmin <- 52

housing_spec <- nearest_neighbor(weight_func = "rectangular", neighbors = kmin) |>
  set_engine("kknn") |>
  set_mode("regression")

housing_fit <- workflow() |>
  add_recipe(housing_recipe) |>
  add_model(housing_spec) |>
  fit(data = housing_train)

housing_summary <- housing_fit |>
  predict(housing_test) |>
  bind_cols(housing_test) |>
  metrics(truth = price, estimate = .pred) |>
  filter(.metric == 'rmse')

housing_summary

A tibble: 1 × 3
.metric	.estimator	.estimate
<chr>	<chr>	<dbl>
rmse	standard	83214.71

# Predicted values on our test data

housing_preds <- predict(housing_fit, housing_test) |>
  bind_cols(housing_test)

# Plot the fitted regression line

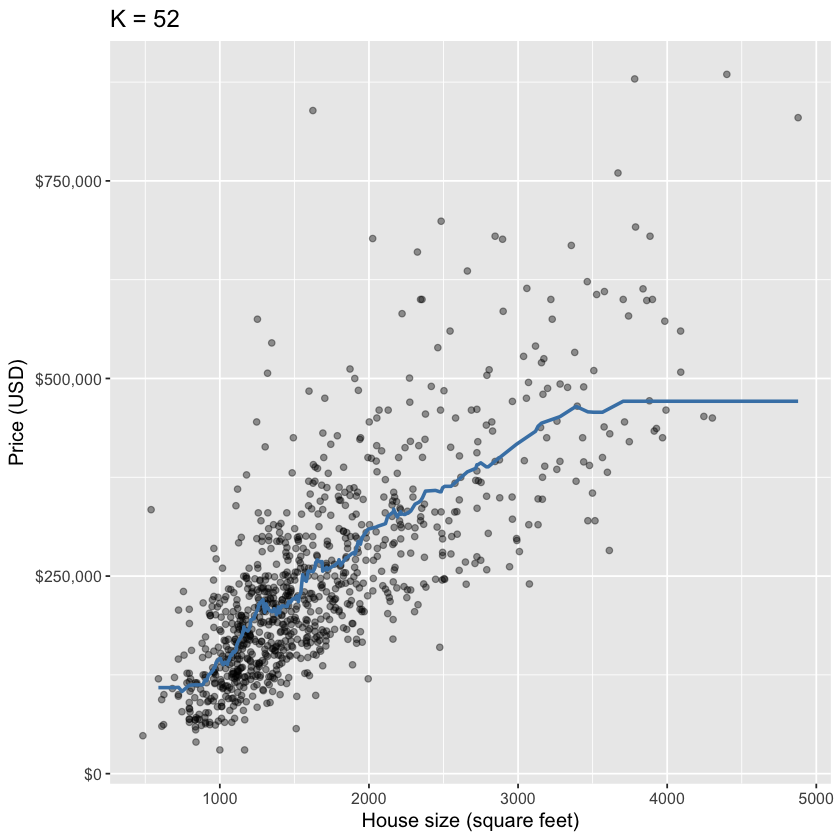
plot_final <- ggplot(housing, aes(x = sqft, y = price)) +
  geom_point(alpha = 0.4) +
  geom_line(data = housing_preds,
            mapping = aes(x = sqft, y = .pred),
            color = "steelblue",
            linewidth = 1) +
  xlab("House size (square feet)") +
  ylab("Price (USD)") +
  scale_y_continuous(labels = dollar_format()) +
  ggtitle(paste0("K = ", kmin)) +
  theme(text = element_text(size = 12))

plot_final

../_images/c6ba7b74d7249888dbf545267b0d5d8662cc0f0eec380a2ed3becb1df1252eef.png

Final model from k-nn regression#

For this model, RMSPE is 83,214.71. How can we interpret this?

Roughly, prices tend to be +/- $83,214.71 off that line (not that great).

Discussion: Which of the following is overfitting? Underfitting?#

https://datasciencebook.ca/_main_files/figure-html/07-howK-1.png

Day 3 - Girls in Data Science

Contents

Day 3 - Girls in Data Science#

Day 3 Learning Objectives#

1. Classification#

What kind of data analysis question is this?#

1.2 Training and Test Sets#

Golden Rule of Machine Learning / Statistics:#

1.3 K-nearest neighbours classification#

What would the predicted class be?#

We can go beyond 2 predictors!#

1.4 Standardizing Data#

Nonstandardized Data vs. Standardized Data#

1.5 tidymodels package in R#

1. Make a recipe to specify the predictors/response and preprocess the data#

2. Build a model specification (model_spec) to specify the model and training algorithm#

3. Put them together in a workflow and then fit it#

4. Predict a new class label using predict#

1.6 How to measure classifier performance?#

Accuracy#

Precision and Recall#

In-class Question#

1.7 Choosing K (or, “tuning’’ the model)#

Cross-Validation#

Underfitting & Overfitting#

Underfitting & Overfitting#

Underfitting & Overfitting#

1.8 Compute performance metrics#

The Big Picture#

Question#

Activity#

2. Regression#

2.1 K nearest neighbours regression#

2.2 Model Evaluation and Tuning#

Is our model any good?#

Final model from k-nn regression#

Discussion: Which of the following is overfitting? Underfitting?#

1.5 `tidymodels` package in R#

1. Make a `recipe` to specify the predictors/response and preprocess the data#

2. Build a model specification (`model_spec`) to specify the model and training algorithm#

3. Put them together in a workflow and then `fit` it#

4. Predict a new class label using `predict`#